Derivadas
En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se toma cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
El concepto de derivada es uno de los dos conceptos centrales del cálculo infinitesimal. El otro concepto es la «antiderivada» o integral; ambos están relacionados por el teorema fundamental del cálculo. Quizá la derivada es el concepto más importante del Cálculo Infinitesimal.
Fórmulas de derivación
Derivada de una constante
Derivada de x
Derivada de la función lineal
Derivada de una potencia
Derivada de una raíz cuadrada
Derivada de una raíz
Derivada de una suma
Derivada de una constante por una función
Derivada de un producto
Derivada de la función exponencial
Derivada de la función exponencial de base e
Derivada de un logaritmo
Como también se puede expresar así:
Derivada de un logaritmo neperiano
Derivada del seno
Derivada del coseno
Vídeos sobre como resolver una derivada :
Integrales
Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).
Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) tales que:
F'(x) = f(x).
Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.
[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)
Ademas es el proceso que permite restituir una función que ha sido previamente derivada. Es decir, la operación opuesta de la derivada así como la suma es a la resta.
Por conveniencia se introduce una notación para la antiderivada de una función
Si F!(x) = f(x), se representa
A este grafo ∫ se le llama símbolo de la integral y a la notación ∫fx dx se le llama integral indefinida de f(x) con respecto a x. La función f(x)se denomina integrando, el proceso recibe el nombre de integración. Al número C se le llama constante de integración esta surge por la imposibilidad de la constante derivada. Así como dx denota diferenciación son respecto a la variable x, lo cual indica la variable derivada.
∫f x dx
Esto se lee integral de fx del diferencial de x
Propiedades de la integración:
· ∫ kfx dx = k ∫f x dx
· ∫ (f x+ gx) dx = ∫f x dx + ∫g x dx
Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.
Una integral indefinida se representa por: ∫ f(x) dx Se lee: integral de x diferencial de x.
Integral indefinida
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de x diferencial de x.
Diferentes símbolos a la hora de integrar:
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.
Linealidad de la integral indefinida
1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx = ∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx
Para mejor aprendizaje en las integrales:
Acá integrales básicas y explicadas :
 Ejercicios:
Ejercicios:
· Es una integral inmediata perteneciente al segundo caso, en el que m = 4.
Resolución:
Cursos de integrales inmediatas para un mejor aprendizaje :
Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla.
Resolución:
Resolución:
Resolución:
Por eso es que se usa para integrales que contienen dos funciones que se multiplican entre si.
Pasos:
Ya que 2 es una constante, podemos fácilmente colocarla fuera de la integral, y nos quedaría:
2 ∫ dx
Calculamos la integral de dx buscando en la tabla la cual = x + c
2 ∫ dx
Calculamos la integral de dx buscando en la tabla la cual = x + c
= 2x+c.
Otro tipo de integral seria la siguiente :
Otro tipo de integral seria la siguiente :
Otro Ejemplo seria :
∫ cosx dx= senx + C
En esta integral se busco tanto la integral de cosx la cual es : senx y dx la cual es = x+c
Integrales inmediatas
Integrales inmediatas son las que salen directamente por la propia definición de integral, es decir, la que se puede resolver de forma más o menos intuitiva pensando en una función que cuando se derive me dé la que está en la integral.
Al igual que se hace con las derivadas, hay una lista de integrales inmediatas, que como puedes comprobar es la contraria de la de las derivadas.
También esta la integral de una constante la cual es la constante por x.
Ejemplo : ∫ 3dx= 3x + c
Integral de cero: ∫ 0 dx = c
Integral de una potencia:

Resolución:
· Es una integral inmediata perteneciente al segundo caso, en el que m = 4.
Resolución:
Resolución:
· Por la propiedad del producto de potencias de la misma base,
Por tanto,
Resolución:
· Es una integral inmediata perteneciente al cuarto caso en el que a = 3.
Métodos de integración
La integración tiene algunos métodos, llamados técnicas de integración que permiten reducir ciertas integrales a otra ya conocidas (la tabla). Entre esas técnicas se tiene el cambio de variable que se estudia a continuación.
Integral por sustitución o cambio de variable
El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
Se comenzará por estudiar aquellas integrales que son casi inmediatas.
Si en lugar de x se tuviese una función u(x), x ® u(x) ® u(x)m , la regla de la cadena
Por tanto,
Como se ve, se ha escrito u en lugar de u(x) por simplificar la notación.
Pasos para integrar por cambio de variable
1º Se hace el cambio de variable y se diferencia en los dos términos:Se despeja u y dx, sutituyendo en la integral:

2º Si la integral resultante es más sencilla, integramos:
3º Se vuelve a la variable inicial:

2º Si la integral resultante es más sencilla, integramos:
3º Se vuelve a la variable inicial:
Ejercicio: cálculo de integrales por cambio de variable
Resolución:
por la constante (en este caso 2) que falta.
Resolución:
Resolución:
· Se multiplica y se divide por 3:
Si en lugar de x se tuviese una función de x, u(x), la derivada de ln | u(x) |, por la regla de
Mas Ejercicios:
Resolución:
· Se multiplica y se divide por 6:
Resolución:
Por tanto,
La derivada de ex es la propia función ex . Si en lugar de x se tuviese una función
u( x ), la derivada de eu( x ) por la regla de la cadena es eu( x ) · u' ( x ).
Por consiguiente,
Vídeos sobre método de integración por cambio de variable :
Integración por partes
El método de integración por partes está basado en la derivada de un producto de funciones como se muestra a continuación
d(u.v) = u dv + v du
∫d(u.v) = ∫u dv + ∫v du (se integra en ambos lados de la fórmula)
(u.v) = ∫u dv + ∫v du (resolviendo la integral)
∫u dv = u v - ∫v du (despejando, queda la fórmula de la integración por partes)
Se llama integración por partes, porque la integral se divide en dos partes una u y otra dv. La integral debe estar completa y sin alterar la operación dentro de ella. Esta selección es lo más importante y se debe realizar de la siguiente manera
1.- En la parte que corresponde a dv debe ser la función más fácil de integrar,
2.- En u deben ir aquellas funciones que no tienen integral directa (funciones logarítmicas e inversas), luego se pueden considerar las funciones algebraicas puesto que la derivada es reductiva. Las funciones trigonométricas y exponenciales son más sencillas de trabajar.
Una de las reglas para saber si el procedimiento realizado es correcto la integral resultante debe ser más sencilla que la original o sino de igual dificultad.
Pasos:
- Se identifica (u) y (dv)
- · Se determina (du) y (v)
- · Se reescribe la integral, de acuerdo a la fórmula de integración por partes
- · Se integra
3er ejercicio
4to Ejercicio
Vídeos sobre como resolver una integral por parte:
Integrales Definidas
Integral definida
Sea f una función que esta definida en el intervalo cerrado [a,b]. Si se dice que f es integrable en [a,b]. Además, denominado integral definida de f desde a hasta b.
Teorema Fundamental de Cálculo

Los pasos para el Teorema fundamental del cálculo
1.-Se verifica el dominio de la función de la integral dentro del intervalo a evaluar. ( el teorema sólo se puede aplicar si la función es continua para todo el intervalo.)
2.- Se resuelve la integral de acuerdo a la función presente, puede ser cualquier método de integración. ( los límites de integración deben concordar con la variable a estudiar, es decir si se realiza un cambio de variable se deben cambiar los límites)
3.- Se debe evaluar la función resultante, sustituyendo los límites superior menos inferior, como se puede ver en la figura es por la diferencia.
Propiedades de la integral definida:

La constante de integración no se coloca en la integrales definidas porque ellas se anulan por ser la diferencia entre los límites.
Ejemplos:

Vídeos sobre integrales definidas












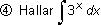


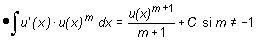





























































No hay comentarios:
Publicar un comentario