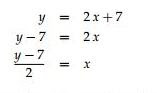Funciones En Matemática
En
matemática, una función (f) es una relación entre un conjunto dado X (llamado
dominio) y otro conjunto de elementos Y(llamado condominio) de forma que a cada
elemento x del dominio le corresponde un único elemento f(x) del condominio
(los que forman el recorrido, también llamado rango o ámbito).
En conclusión
las funciones matemáticas equivalen al proceso lógico común que se expresa como
“depende de”.
Las funciones
matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de
una llamada telefónica que depende de su duración, o el costo de enviar una
encomienda que depende de su peso.
A modo de
ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los
de la izquierda en la siguiente lista?:
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
Los números
de la derecha son los cuadrados de los de la izquierda.
La regla es
entonces "elevar al cuadrado":
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
x --------> x2.
Para referirse
a esta regla podemos usar un nombre, que por lo general es la letra f (de función). Entonces, f es la
regla "elevar al cuadrado el número".
Otro ejemplo
seria:
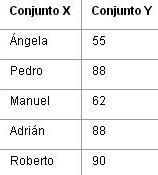
Correspondencia entre las personas que
trabajan en una oficina y su peso expresado en kilos
Cada persona
(perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o
variable independiente. Cada peso (perteneciente al conjunto Y o codominio)
constituye lo que se llama la salida o variable dependiente. Notemos que una
misma persona no puede tener dos pesos distintos. Notemos también que es
posible que dos personas diferentes tengan el mismo peso.
Existen distintos tipos de funciones las cuales son :
Función Lineal
Una función
lineal es una función cuyo dominio son todos los números reales, cuyo codominio
son también todos los números reales, y cuya expresión analítica es un
polinomio de primer grado.
Definición: f: R —> R / f(x) = m.x+b donde m y b son
números reales, es una función lineal.
Este último
renglón se lee: f de R en R tal que f de equis es igual a a.x+b
Definición: Las funciones lineales son polinomios de
primer grado. ver grafica ejes
Recordemos
que los polinomios de primer grado tienen la variable elevada al exponente 1.
Es habitual no escribir el exponente cuando este es 1.
Ejemplos de
funciones lineales: a(x) = 2x+7
b(x) = -4x+3 f(x) = 2x + 5 + 7x - 3
De estas
funciones, vemos que la f no está reducida y ordenada como las demás. Podemos
reducir términos semejantes para que la expresión quede de una forma mas
sencilla, f(x) = 9x + 2
Tambien
recordemos que hemos convenido que cuando no establecemos en forma explicita el
dominio y el codominio de una función, supondremos que es el mayor conjunto
posible en cada caso.
Por ejemplo,
si hablamos de la función f, de dominio real y codominio real, tal que f(x)=
2x-6, anotaremos f: R ——-> R / f(x) =
2x-6 Siendo el dominio todos los números
reales, R, y el codominio también, todos los números reales, R.
Esto se lee
" f de R en R tal que f de x es igual a 2x-6"
Vamos a
graficar esta función, que tal cual lo vimos en la definición, es una función
lineal por ser de primer grado. Para
graficarla haremos una tabla de valores.
f: R ——> R
/ f(x) = 2x-6
Le vamos
dando valores a "x". ¿Que
valores le podemos dar? Cualquiera que
este dentro del dominio.
Por ejemplo,
si x = 5 , entonces f(x) pasa a ser f(5), que es f(5) = 2.(5)-6 f(5) = 4
Entonces al 5
le corresponde el 4. Nuestro punto es
el (5,4).
¿Cómo se
coloca en un par de ejes coordenados?
Si el eje contiene un 0 se traza de la siguiente manera:
Si contiene dos números diferentes a 0 se traza de la siguiente manera dependiendo el signo:
Luego de
darle el valor a la variable a todos los elementos de el dominio y obtenemos
los resultados procedemos hacer la
gráfica de una función lineal. Construyendo
juntos la gráfica de una recta.
Aca nos dan una recta y la formula para sustituir las x :
Le damos valor a A x segun el dominio :
Depende de el rango (resultado de al sustituir la x), unimos los puntos:
En este casco quedo asi :
Función Cuadrática:
Una función
cuadrática es aquella que puede escribirse como una ecuación de la forma:
f(x) = ax2 + bx + c
Donde a, b y c
(llamados términos) son números reales cualesquiera y a es distinto de cero
(puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de
c sí puede ser cero.
En la ecuación
cuadrática cada uno de sus términos tiene un nombre.
Así:
ax2 es el término
cuadrático
bx es el término
lineal
c es el término
independiente
DEFINICIÓN:
Llamaremos función cuadrática a las funciones polinómicas de segundo grado, de
dominio real y codominio real.
y= f(x) = ax²+bx+c con a 0.
Tal como lo vimos
en el tema funciones y en función lineal, si no se dice lo contrario,
suponemos, o convenimos, que estamos trabajando con todos los números reales.
En lenguaje
matemático, nuestro dominio es el conjunto de los números reales.
Ejemplos de
funciones cuadráticas:
A(x) =
3x²+5x-8 P(x) = -2x²-7x+1 C(x) = x²-1 D(x) =
-x²
A la hora de graficar una función cuadrática debemos saber
que siempre será una parábola, esta parábola va a cambiar depende del signo de
a en la función:
ax²+bx-+c
Si a > 0
(positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2
− 3x − 5
Grafica
Si a < 0
(negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2
+ 2x + 3
Para empezar a construir la parábola debemos primero conocer
los Puntos de corte con el eje X
En el eje de abscisas la segunda coordenada es cero, por lo
que tendremos:
ax² + bx +c = 0
Quedándonos de la siguiente manera.
f(x)= ax² + bx +c =0
Además de ellos debemos tener claro que unos de los pasos
para resolver la ecuación es teniendo el vértice:
Un punto importante en la grafica de una función cuadrática
es el vértice de la parábola, conociendo el vértice podemos orientarnos en el
momento de hacer la grafica.
En el análisis de ciertos problemas también es importante
conocer el vértice de la parábola.
El vértice de una función se saca con la siguiente formula:
b/2.a=
Otra de las funciones que usamos es la discriminante.
DISCRIMINANTE: En la fórmula de Bháskara aparece la raíz
cuadrada del término b²-4.a.c que lo usaremos
mucho. A este término se le llama
discriminante, porque no ayuda a discriminar si la función cuadrática tendrá o
no raíces reales. Vamos ahora a ver como se hace esto. ¿Cuándo existe una raíz cuadrada? ¿Siempre se puede hacer esta operación? Dicho
de otra forma, ¿a cuáles números se les puede calcular la raíz cuadrada?
Como en la fórmula de Bháskara aparece una raíz cuadrada,
ésta se podrá hacer siempre que el número al que se la apliquemos sea positivo,
o cero.
Para resolver una función cuadrática podemos aprender a resolverla con este video:
Función Racional
Las funciones racionales son
expresiones que tienen forma
parecida a los números racionales
o fraccionarios, como también se les conoce,
un numerador y un denominador, en
el caso que vamos a estudiar estos términos serían funciones. También se les conoce como
funciones polinómicas porque sus términos son polinomios. Atendiendo a estos
señalamientos la función racional se expresa de la siguiente manera:
Los más usuales son:
1. Funcion donde el
numerador es una constante y el
denominador un monomio de grado
1.
Es una función racional, debido a que su numerador es la
función constante y su denominador es la función identidad.
2. Función donde el
numerador es una constante y el denominador
un binomio de grado 1.
En este caso el valor 3 para x anula el denominador por lo
que f(x) existe para x diferente de 3.
Tanto el numerador como el denominador pueden ser cualquier
polinomio, siempre y cuando no existan valores para la o las variables que anulen el denominador,
es decir el denominador debe ser diferente de cero.
Dominio y rango de la función racional.
a. El dominio de la función racional, está formado por todos
los valores de “x” en donde la función esté definida.
Como la división por cero no está definida, se excluyen del
dominio los valores de “x” que anulan el denominador.
En el ejemplo:
Para hallar su dominio se excluyen los valores de x que
anulen el denominador y para ello se iguala a cero este último.
En la gráfica vemos que:
Entre -00 y 0 la curva
varía entre 0 y -00, es decir,
cuando x se acerca a 0, f(x) se aproxima a -∞ y cuando x se aproxima a -00 f(x)
se acerca a 0, siendo 00 el símbolo de infinito.
Entre 0 y +00 la
curva varía entre 0 y +00, es decir, cuando x se acerca a 0, f(x)
se aproxima a +00 y cuando x se aproxima a +00 f(x) se acerca a 0.
Cuando la función toma el valor de cero, no existe; ya que
la división por cero no está definida.
Entonces el Dominio de esta función está formado por todos
los números reales menos el cero, es decir Dom
f(x) = IR - { 0 }.
También se dice, que en x = 0 la función tiene una asíntota
vertical.
Para hallar el rango de la función racional se despeja la
variable “x” en función de “y” y se hace el mismo procedimiento que para hallar
el dominio.
Como y = f(x) nos queda que:
Luego f(x) debe ser diferente de 0 (f(x) ≠ 0), por lo tanto
el Rango de la función en cuestión, es el conjunto de todos los números reales
menos el 0. Ranf(x) = IR - { 0 }.
En el caso de la función f(x) = 2/(x-3) cuya gráfica es la
que se presenta a la izquierda, el
Dominio se halla de la misma forma:
a. Igualamos el denominador a cero.
x - 3 = 0, x = 3
El Dominio y el Rango se determinan de la forma siguiente:
Dominio
Dom f(x) = IR - { 3 }
Rango
Despejamos x en la ecuación:
Aquí también aplicamos el criterio de que f(x) = y debe ser
diferente de 0, por lo que el Rango queda definido de la forma siguiente.
Ran f(x) = IR - { 0 }
La gráfica de una función racional deberá ser parecida o de la misma forma que esta gráfica:
Como resolver una función racional:
Función Inversa
Una función es una relación entre
dos variables, de manera que para cada valor de la variable independiente
existe a lo más un único valor asignado a la variable independiente por la
función.
Imagina que tienes la función y =
f(x). Tú le das un valor (x) y ella te devuelve otro (f(x)).
Una buena idea sería encontrar
una función que cuando le demos el valor f(x) nos devolviera x, es decir, una
máquina que haga la transformación inversa de f(x).
En otras palabras, queremos
encontrar una función que deshace la transformación que ocasiona la función f
sobre los números que le damos.
Función inversa:
Sea f una función con dominio Xf
y contradominio Yf. Si existe una función g con dominio Xg y contradominio Yg
tal que:
i. f(g(x)) = x para toda x 2 Xg
ii. g(f(x)) = x para toda x 2 Xf
Entonces decimos que las
funciones f y g son inversas una de la otra.
f^-1 Denota
la función inversa de f .
En otras palabras, si
intercambiamos las coordenadas de los pares formados por (x, f(x)) obtenemos
(f(x), x), que no son sino los puntos de la función inversa f1
Es decir, el dominio de f es el
contradominio de f1 y el contradominio de f es el dominio de f1
Aca podemos ver su definición
mejor explicada:
No todas las funciones tienen
función inversa. Esto se debe a la definición de función.
Para que una relación sea
considerada función, para cada elemento del dominio le debe corresponder a lo
más un elemento del contradominio.
Si una función debe tener función
inversa, a cada elemento del contradominio le debe corresponder a lo más un
elemento del dominio (por definición de función inversa).
En otras palabras, para cada
elemento del dominio de f le corresponde un elemento de su contradominio y
viceversa.
Quiere decir que si una función
tiene inversa, entonces es uno a uno y viceversa, si una función es uno a uno,
entonces tiene inversa. Si y 0 está en el contradominio de la función f ,
entonces este valor tiene asociado un único valor x0 a partir del cual se le
calculó usando f . Es decir, y0 = f(x0).
Si definimos la función g que toma
como su dominio al contradominio de f y asignamos al contradominio de g los
elementos del dominio de f , estamos diciendo que g es la función inversa de f
.
Tanto f como g son funciones (una
inversa de la otra) porque cumplen con la condición de que a cada elemento del
dominio le corresponde a lo más un elemento del contradominio», impuesto por la
definición de función.
Para calcular la función de la
inversa se mostraran los siguientes pasos :
·
Por definición de función inversa, para cada x le
corresponde un y y viceversa.
·
La función «directa» es: y = 2 x + 1.
·
La función inversa «deshace» la transformación,
es decir, le damos y y ésta nos devuelve x.
·
En otras palabras, la variable dependiente de la
función «directa» viene siendo la variable independiente de la función inversa.
·
Y la variable dependiente de la función
«directa» juega el papel de la variable independiente en la función inversa.
·
Así que vamos a despejar x en términos de y.
Esta expresión puede verse como
una función: nosotros le damos el valor de y y ésta nosdevuelve el valor de x.
·
Ahora cambiamos las variables para que se trate
de la función inversa:
·
Ahora Vamos a verificar que el resultado del
ejemplo anterior es correcto. Para eso, vamos a calcular valores de y para la
función «directa» y después vamos a hacer los cálculos respectivos para la
función inversa.
Ahora veremos con un video como
resolver mejor la función inversa :
Función Exponencial
La función exponencial que tiene como base el numero e, se
le denomina como función exponente natural y es la función expresada por:
F(x)= e^x.
En donde e es un numero irracional que puede expresarse con
cualquier grado de exactitud usando una serie infitnita.
Esta función tiene por dominio de definición el conjunto de
los números reales, y tiene la particularidad de que su derivada es la misma
función. Se denota equivalentemente como :
F(x)=ex o exp(x), donde e es la base de los logaritmos
naturales y corresponde a la función inversa del logaritmo natural.
.
Propiedades de la función exponencial :
Como colocar el numero e en la calculadora:
Gráfica de una función exponencial:
Como resolver una función exponencial:
Función enesima
o radical
Por funciones radicales entendemos aquellas que llevan una
raíz en su definición. Dicha raíz puede ser cuadrada, cúbica, cuarta…Pero en
este curso, por sencillez, nos limitaremos a raíces cuadradas. Trabajaremos
además sólo con funciones de la forma con a y b tomando valores cualesquiera
(pero , pues en caso contrario no tendríamos x debajo de la raíz y ya no sería
una función radical). Recordemos, además que una raíz cuadrada siempre tiene
dos signos, positivo y negativo, pero por la definición de función, a cada x
sólo le puede corresponder una y. Si tomáramos los dos signos de la raíz,
obtendríamos como "representación" de esta relación algo así como
esto:
Propiedades de esta funcion :
Como resolver una función radical: